10) Diviseurs

U n nombre est un diviseur d'un autre nombre s'il se le divise exactement.
Donc, 6 est un diviseur de 18, car il le divise exactement trois fois.
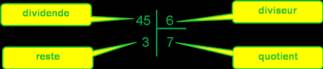
Dans ce genre d'opération, le nombre divisé, 18, est le dividende.
Qu'en est-il du 19 divisé par 6 ? Dans ce cas, 6 n'est pas un diviseur de 19, car il le divise trois fois, mais en laissant de plus 1. 1 est le reste de la division de 19 par 6.

Pour deux nombres p et q, le plus grand commun diviseur [PGCD] est le plus grand nombre qui est un diviseur de p et de q.
 Puisque 1 est manifestement un diviseur des deux nombres, le PGCD est toujours plus grand ou égal à 1.
Si le PGCD est 1, les nombres sont co-premier,  ils n'ont en commun aucun diviseur positif, à l’exception de 1.
Les diviseurs de 18 sont : 1, 2, 3, 6, 9, 18
Les diviseurs de 30 sont : 1, 2, 3, 5, 6, 10, 30
le PGCD de 18 et 30 est 6
 

Les diviseurs donnent naissance à une famille intéressante, les nombres parfaits.
Ce sont des nombres dont la somme de leurs diviseurs positifs, à l'exclusion d'eux-mêmes, est égale au nombre lui-même.
Le premier nombre parfait est 6            : 1 + 2 + 3 = 6.
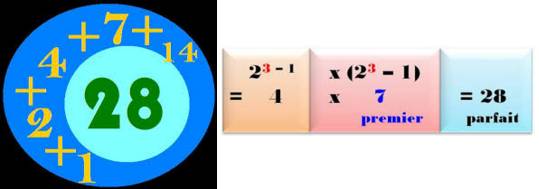
Le second nombre parfait est 28            : 1 + 2 + 4 + 7 + 14 = 28
Le troisième nombre parfait est 496     : 1+2+4+8+16+31+62+124+248 = 496.
Les nombres parfaits sont rares et difficiles à trouver.
Les mathématiciens n'ont pas encore découvert des réponses probantes à certaines questions importantes du genre y a-t-il un nombre infini de nombres parfaits, ou tous les nombres parfaits sont-ils pairs.