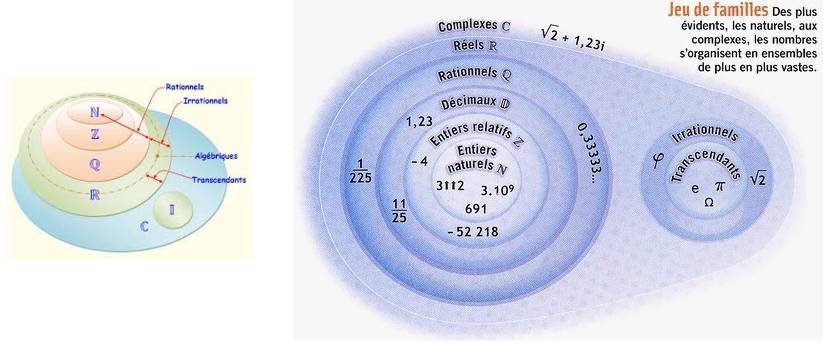
13) Nombres algébriques et transcendants
Un nombre algébrique est un nombre complexe qui est la racine d'un polynôme [équation impliquant des puissances de la variable x] à coefficients rationnels.
Un nombre transcendant n'est pas algébrique. Les coefficients de telles équations sont les nombres qui multiplient chacune des variables.
Par exemple, √2 est irrationnel, car il ne peut pas être écrit en tant que rapport de deux nombres entiers.
Mais il est aussi algébrique, car il est la solution de l'équation x2 - 2 = 0.
Tous les nombres rationnels sont algébriques, car tout rapport donné p/q peut être une solution de q x - p = 0.
On s'attendrait à ce que les nombres transcendants soient rares, alors que c'est le contraire. √2 est exceptionnel, presque tous les nombres irrationnels sont aussi transcendants.
Très difficile à prouver, un nombre choisi au hasard entre 0 et 1 sera presque assurément transcendant.