23) Théorème de Pythagore

 

Bien qu'elle soit nommée d'après le mathématicien grec Pythagore de la fin  du VI siècle av. J.-C, cette célèbre relation entre les longueurs des côtés d'un triangle rectangle était presque assurément connue des siècles plus tôt chez les Babyloniens.

 

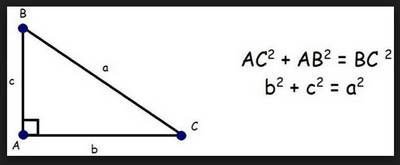
Le théorème ne prône que le carré du côté le plus long, l'hypoténuse, est égal à la somme des carrés des longueurs des deux autres côtés.

 

 

 

 

 

 

 

 

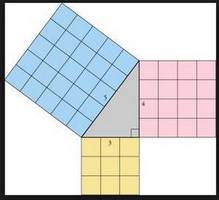
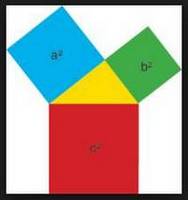
Une démonstration simple reposant sur les rapports des côtés de triangles semblables est montrée ci-dessous, mais le théorème peut aussi être démontré en considérant les aires des carrés géométriques construits sur chaque côté du triangle.

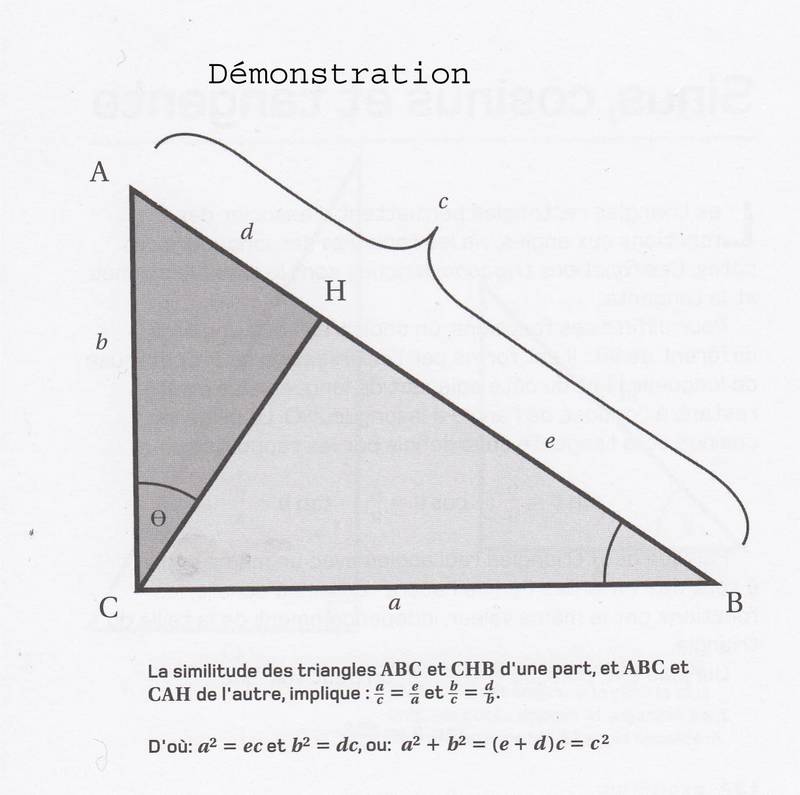
Le théorème de Pythagore est un outil important de la géométrie. Plusieurs dénitrions de la distance en coordonnées cartésiennes sont basées sur cette relation, qui peut être reformulée en termes de relation entre les fonctions trigonométriques sinus et cosinus (sin²(x) + cos²(x) = 1).